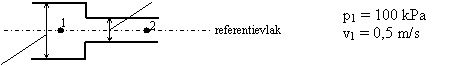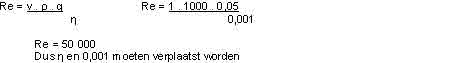Wet van Bernoulli

De wet van Bernoulli is in feite niets anders dan de wet van Behoud van Energie
De wet gaat uit van een ideale stationair stromende vloeistof. Dit is een vloeistof die niet samendrukbaar is en er tussen de vloeistofmolekulen geen sprake is van wrijving.
Bernoulli zegt dan over de in onderstaand figuur aangegeven situatie:
De energie in een bepaalde hoeveelheid vloeistof is op plaats 1 gelijk aan die op plaats 2.

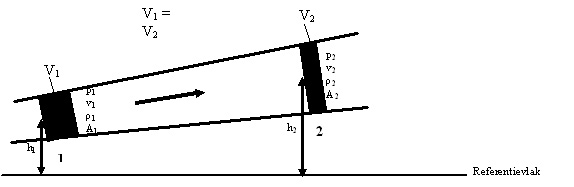
Dit betekent:   p₁.V₁+ ½ mv₁² + m.g.h₁ = p₂.V₂ + ½mv₂² + m.g.h₂

m=V.ρ. dus:     p₁.V₁+ ½ V₁.ρ.v₁² + V₁.ρ.g.h₁ = p₂.V₂ + ½ V₂.ρ.v₂² + V₂.ρ.g.h₂

V₁ = V₂ dus:    p₁ + ½.ρ.v₁² +.ρ.g.h₁ = p₂ + ½.ρ.v₂² + ρ.g.h₂

Ofwel:             p + ½.ρ.v² +h.ρ.g = constant

In woorden luidt de wet van Bernoulli:

Toepassingen van de Wet van Bernoulli:

Wanneer we onderin een groot open vat een klein gaatje van 2 cm² boren kunnen we de uitstroomsnelheid van het water door dit gaatje berekenen.

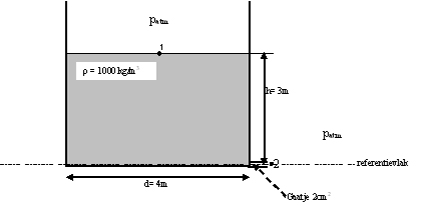
Volgens de Wet van Bernoulli geldt t.o.v. het referentievlak:

p₁ + ½.p.v₁² +.p.g.h₁ = p₂ + ½.p.v₂² + p.g.h₂

De daalsnelheid van het niveau bij punt 1 en de hoogte van punt 2 t.o.v. het referentievlak kun je op “nul” stellen. Dan geldt:

p₁ + p.g.h1 = p₂ + ½.p.v₂²

Ook geldt: p₁ = p₂ (omgevingsdruk) en dus geldt ook:

h₁.p.g          = ½.p.v₂²
3 . 1000 . 10 = ½ . 1000 . v²
30.000         = 500 . v²
v²               = 60
v                 = 7,75 m/s

Oefenopgave: Reken voor onderstaande geschetste situatie uit wat de stroomsnelheid en de druk in punt 2 zijn.

                                                                   d₂ = 2,5 cm

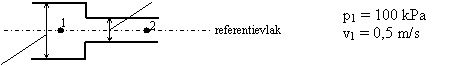
                 d₁ = 5 cm  

Uitgaande van de wet van Bernoulli en de berekende uitkomst van de oefenopgave kunnen we dus concluderen dat tengevolge van een vernauwing in een leiding de stroomsnelheid toeneemt en de statische druk in dit versmalde deel van de leiding afneemt


Reynoldsgetal en wrijvingscoëfficienten

Bernoulli gaat uit van ideale vloeistoffen. In werkelijkheid zijn vloeistoffen nooit ideaal en hebben we te maken met inwendige wrijving, ofwel viscositeit van vloeistoffen.

Het gevolg van deze inwendige wrijving is dat we bij stroming van vloeistoffen verschillende stromingsprofielen kennen. Zo kan een vloeistof zich door een leiding verplaatsen met een laminair of een turbulent stomingsprofiel. Deze twee stromingsprofielen zijn in onderstaande figuur weergegeven.



Met welk stromingsprofiel een vloeistof zich verplaatst wordt bepaald door de gemiddelde stromingssnelheid in de leiding, inwendige diameter van de leiding, dichtheid en dynamische viscositeit van de vloeistof. Het verband hiertussen ligt vast in het Reynoldsgetal Re.

Het Reynoldsgetal is een dimensieloos getal en er geldt:

Re ≤ 3000(2300)  : stroming is laminair
Re ≥ 6000           : stroming turbulent
3000 ≤ Re ≤ 6000 : overgangsgebied

Of een stoming laminair of turbulent is heb je onbewust wel eens waargenomen. Zet je namelijk de waterkraan thuis een klein beetje open, dan is de waterstraal doorzichtig. De stroming is dan laminair. Wanneer je de kraan steeds verder open zet wordt de straal op een gegeven moment ondoorzichtig. De stroming is dan turbulent.

Links in bovenstaande figuur zien we laminaire stroming en rechts zien we turbulente stroming.

Rekenvoorbeeld: Door een leiding met een inwendige diameter van 5 cm stroomt water met een snelheid van 1 m/s. De dichtheid van water is 1000 kg/m3 en de dynamische viscositeit van water is 0,001 Pa.s.
Is de stroming laminair of turbulent?

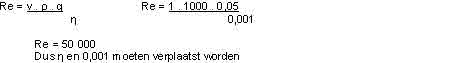
De stroming in de leiding is dus turbulent.

Vloeistoffen zijn nooit ideaal, hetgeen betekent dat zij tijdens stroming ook wrijving met de leidingwand ondervinden. Hierdoor gaat er energie verloren hetgeen zich manifesteert als een drukverlies over de leiding.
De grootte van dit drukverlies kunnen we berekenen met de formule:



Het wrijvingscoëfficient λ is afhankelijk van de de relatieve ruwheid ε/d van de binnenzijde van de leiding en het reynoldsgetal. Deze wrijvingscoëfficient λ kunnen we vinden met behulp van het Moody-diagram.



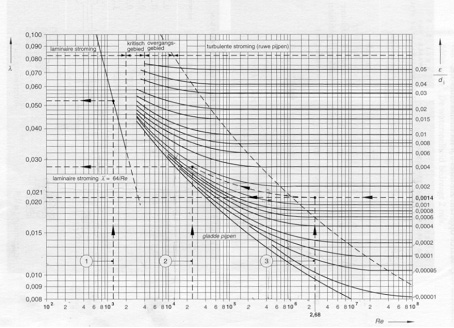
Je ziet in het Moody-diagram dat bij een turbulente stroming met een Reynoldsgetal van 2,68 x 10⁶en een relatieve leidingruwheid ε/d_i ( ε is de absolute buisruwheid en d_i de inwendige diameter van de buis ) van 0,0014 je een wrijvingscoëfficient λ vindt van 0,0205.

Voor de berekening van het drukverlies over bochtstukken en appendages, zoals afsluiters, maken we meestal gebruik van de formule:



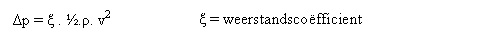
En ξ staat hier in principe voor λ . l/d.
De waarde van ξ kunnen we onder andere vinden in tabellen, zoals hieronder weergegeven.

Ook worden er voor bochtstukken en appendages equivalente pijplengten gegeven, zodat we de ξ-waarde met behulp van ξ = λ. l/d kunnen berekenen.